3) Dynamic Programming, Policy Evaluation, Iteration

Policy Evaluation: 평가에 대한 문제

Policy Iteration: 반복을 통한 최적화에 대한 문제

 

 

Dynamic Programming:

solve the subproblems + combine solutions to subproblems

작은 문제들로 나누어 풀고, 하나로 모아 문제를 해결

 

 

DP Two Properties:

optimal substructure & overlapping subproblems

optimal solution can be decomposed into subproblems

subproblems recur many times, soluitons can be cached and reused

작은 문제들로 나눌 수 있고, 작은 문제들이 다시 나타나기 때문에 잠깐 저장해 두었다가(cached) 다시 사용할 수 있다.

 

MDP는 위의 조건을 만족한다. 따라서 dynamic programming으로 planning에 사용 가능하다.

 

 

 

 

 

 

 

 

Policy Iteration:

 

Iterative Policy Evaluation:

 

termianl state는 2개, 보상은 0, discount는 1로 왼쪽은 value function evaluation, 오른쪽은 policy improvement 

 

위의 그림처럼 벨만 기대 방정식(현재 상태와 다음 상태의 value function에 대한 관계식)을 계산해서 모든 상태의 value를 구할 수 있다. 그리고 Iterative 하게 value를 조금씩 개선해 가면서 Evaluation을 할 수 있다.

 

 

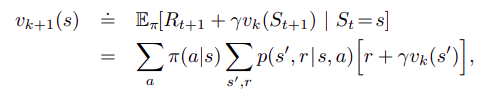
벨만 '기대' 방정식은 다음과 같은 의미를 갖는다. agent는 현재 state에서 취할 수 있는 모든 action과 state를 알고 있다. (MDP의 policy evaluation 문제에서는 state, state transition posability 등 필요한 모든 정보를 안다고 가정한다) 이때 agent는 여러 개의 action 중에 어떤 action이 가장 좋은지, 어떤 행동을 하는 것이 앞으로 받게 되는 보상을 최대로 만들 수 있을 것인지 고민해야 한다. (이 과정이 최적의 policy를 찾는 과정이며 evaluation에서는 단순히 true value function을 찾는 과정이지만, 뒤의 Improvement에서는 value-action function을 사용해서 optimal policy를 찾는다.)

 

따라서 total reward(value)를 최대로 하기 위해서는 어떤 action을 취함으로써 다음 state에 도달했을 때, state가 변함과 동시에 받게 되는 reward와 그 state에서 다음 행동을 했을 때 얻을 수 있을 것이라 예상되는 모든 보상의 기댓값을 더해서 최대가 되는 action을 선택해야 한다. 즉, state transition이 발생할 때 바로 얻을 수 있는 즉각적인 보상뿐만 아니라, 다음 시점에 받을 것이라 예상되는 모든 보상까지 함께 생각해야 한다는 것이다. 이것을 관계식으로 표현한 것이 벨만 기대 방정식이다. 이때 주의할 점은 당장 받는 보상이 아닌, 다음 행동을 했을 때 얻을 것이라 예상되는 모든 보상은 discount factor를 곱해야 하고, stochastic 한 환경에서는 같은 action을 하더라도 다른 state가 될 수 있기 때문에 기댓값으로 표현해야 한다.

 

Policy Evaluation은 일정 Iteration에 도달하면 true value function에 수렴한다. 하지만 모든 value function을 반복적으로 구하는 것은 dynamic programming의 계산을 복잡하게 만들고, model을 알고 있어야만 하기 때문에 한계가 명확하다. Learning은 이러한 문제점들을 보완하고 있다.

 

 

 

Policy Improvement:

 

value를 구하면 policy를 찾을 수 있고, policy를 판단하고 개선해서 optimal policy에 도달할 수 있다. 이 과정을 Policy Improvement라고 한다. Policy Evaluation으로 모든 state의 true value를 구한 후에, action-value function을 이용하여 q function을 구한다. 그리고 이 q-function에서 max 값을 선택해서 greedy optimal policy를 찾을 수 있다. 즉, 단순히 value가 최대가 되는 행동을 greedy 하게 선택하기만 하면 optimal policy에 도달할 수 있다. 여기서 중요한 것은 초기의 policy가 아무리 바보 같은 policy라 하더라도, evaluation과 improvement를 반복했을 뿐인데 true value function을 찾고 optimal policy에 도달한다는 것이다. (증명은 아래 링크 참고)

 

 

 

 

 

 

 

 

 

 

 

Value Iteration:

 

Problem	Bellman Equation	Algorithm
Prediction	Bellman Expectation Equation	Iterative Policy Evaluation
Control	Bellman ExpectationEquation + Greedy Policy Improvement	Policy Iteration
Control	Bellman Optimality Equation	Value Iteration

 

Value Iteration은 Bellman "Optimality" Equation을 사용한다. 위의 Policy Iteration에서 Bellman "Expectation" Equation을 사용할 때 next state에서의 예상되는 보상을 모두 더했다. 그러나 Bellman "Optimality" Equation에서는 max 값을 더해서 greedy 하게 value function을 구한다. 그래서 action 확률을 곱하지 않고 다음의 식을 사용한다.

 

 

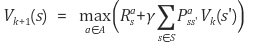
Value Iteration은 policy improvement가 없다. Policy Iteration에서는 stochastic한 환경 때문에 expectation으로 계산했다. 하지만 Value Iteration에서는 현재 policy가 optimal 하다고 가정하기 때문에 max를 취하고 deterministic 한 action으로 생각할 수 있다. 여기서 policy evaluation 안에 policy improvement가 포함된다. 따라서 Value Iteration에서는 policy evaluation만으로도 optimal policy를 찾을 수 있다. 

 

optimal policy 관련 참고:

2020/09/04 - [공부/강화학습] - MDP, Value Function, Bellman Equation

 

 

 

 

 

 

Asynchronous:

 

위의 예시들은 모두 parallel하게 state가 backup되는 synchronous backup 방식이다. 하지만 asynchronous backup 방식으로 몇 개의 state만 backup하면 복잡한 계산을 줄일 수 있다. asynchronous backup을 무수히 많이 했을 때 모든 state들이 selected 된다면 converges 된다는 것이 증명되었다. asynchronous에는 3가지 방법이 있다.

 

In-place dynamic programming: 리스트를 늘리지 않고 하나의 리스트만 가지고 업데이트한다.

Prioritised sweeping: 우선순위를 두고 업데이트한다. 첫 번째 테이블과 두 번째 테이블 값의 차이가 크면 Bellman Error가 큰 것이고 중요한 값이다. priority queue를 이용해서 쉽게 구현할 수 있다.

Real-time dynamic programming: agent를 이용해서 agent가 방문한 state를 업데이트한다.

 

그리고 DP는 Full-Width backups이다. value function을 구할 때 s에서 모든 s'의 값을 참조했다. 이 방법은 비용이 너무 많이 든다. 그래서 큰 문제에서는 sample backups를 사용한다. sample backups는 model free(next state를 모르는 경우)에서도 사용할 수 있다는 큰 장점이 있다.

 

 

 

 

 

 

 

 

참고:

youtu.be/Nd1-UUMVfz4

medium.com/@edu.pignatelli/iterative-policy-evaluation-33056f3f21a4

Iterative policy evaluation

youtu.be/rrTxOkbHj-M